
Fibonacci viene tutt’oggi ricordato per le sue eccezionali doti nel campo della matematica che applicò e rese particolarmente
preziosa nell’ambito dei rapporti commerciali con il mondo arabo, dal quale apprese e utilizzò con estremi frutti il sistema numerico indo-arabo, che ha cambiato il modo di pensare e di conoscere in tutto l’Occidente.
Pisano di nascita, Fibonacci che significa figlio di Bonacci Guglielmo, appartiene ad una famiglia di mercanti della Repubblica Marinara di Pisa. Siamo a cavallo tra XII e XIII secolo, precisamente nel 1175, anno della sua nascita. Determinanti per l’approfondimento delle sue nozioni in campo matematico sono stati i viaggi commerciali intrapresi in Algeria orientale.
La rivoluzione realizzata nel campo della matematica non solo dell’epoca ma fino ai giorni nostri ha di gran lunga semplificato l’aspetto contabile dei mercanti dell’epoca, svantaggiati per l’uso a volte tortuoso dei numeri romani che lasciavano spazio a errori di interpretazione e trascrizione. Ciò che vogliamo raccontarvi però è stata la sua straordinaria scoperta che è stata applicata nelle arti e in architettura ma soprattutto straordinaria in quanto si è dimostrato che essa è presente in natura in numerose forme, da quelle animali a quelle vegetali. Con Altrarealta.com scopriamo la meravigliosa sezione aurea, detta anche proporzione divina.
Sezione aurea di Fibonacci: il numero su cui si regge il mondo
La sezione aurea o rapporto aureo o numero aureo di Fidia, chiamato anche proporzione divina, è un numero irrazionale che si ottiene effettuando il rapporto tra due lunghezze disuguali delle quali la maggiore misura, a, è medio proporzionale tra la misura minore, b, e la somma delle due (a+b). si indica con la lettera greca phi ed è rappresentato dalla seguente formula:
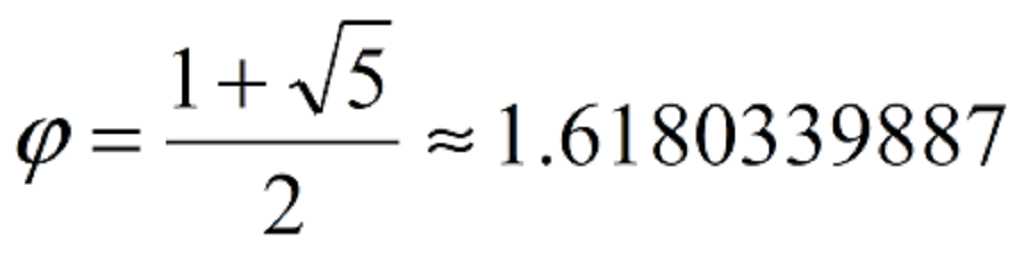
Partiamo dalla elaborazione di una successione numerica, individuata proprio da Leonardo Fibonacci nel 1202, che si rendeva funzionale alla risoluzione di un problema relativo alla evoluzione annuale della popolazione dei conigli: quante coppie di conigli si ottengono in un anno da una sola coppia di partenza, supponendo che essa produca ogni mese, ad eccezione del primo, una nuova coppia che, a sua volta prolifica a partire dal secondo mese?
La risposta è 144 coppie di conigli. In questa serie ogni numero è il risultato della somma dei due numeri precedenti: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… andando così avanti all’infinito.
Facendo il rapporto tra due numeri consecutivi della serie di Fibonacci, tale rapporto approssima sempre meglio il numero aureo.
Numero aureo di Fibonacci in natura e nelle arti
La proporzione divina individuata da Leonardo Fibonacci è nota sin dai tempi più antichi, utilizzata per ottenere una dimensione armonica delle cose. E’ singolare notare come questa proporzione venga riscontrata anche in natura. Partiamo dal frattale, ossia da una figura geometrica nella quale un motivo identico si ripete in ogni direzione e a scala continuamente ridotta. Ciò significa che ad ogni ingrandimento della figura si otterranno forme ricorrenti e ad ogni ingrandimento saranno visibili nuovi dettagli. In ogni ingrandimento la stessa figura è riprodotta in scala.
La serie di Fibonacci si ritrova nell’ordinamento di foglie su un ramo mentre l’ordinamento dei semi o stami di alcuni fiori. Ma qual è il meccanismo che genera tale ordinamento, definito propriamente fillotassi? Nel regno vegetale, la foglia cerca di occupare posizioni sempre migliori al fine di una maggior esposizione all’acqua, all’aria e al sole. Tale successione di foglie e rami ha una componente rotatoria che, andando verso l’alto, traccia attorno al fusto una forma elicoidale immaginaria. Partendo da una qualsiasi foglia, dopo vari giri attorno alla spirale si troverà sempre una nuova foglia allineata alla prima e, a seconda della specie, sarà la seconda, la terza, la quinta, l’ottava, etc. Stessa cosa accade se osserviamo l’andamento a spirale aurea delle brattee delle pigne o anche dei cavolfiori. Si pensi al mondo dei fiori, molti dei quali hanno un numero di petali contenuti nella serie di Fibonacci (giglio 3 petali, ranuncolo 5 petali, speronella 8 petali, cicoria 21 petali, ecc.).
Anche nel corpo umano sono presenti numerosi rapporti aurei: si pensi alle dita della mano, ove i rapporti tra le lunghezze delle falangi di anulare e medio sono aurei. Anche il viso presenta numerosi rapporti aurei:
- Altezza/larghezza del viso.
- Linea occhi rispetto a mento e fronte.
- Posizione bocca rispetto a mento e occhi.
- Altezza e larghezza naso.
- Lunghezza e altezza del profilo della bocca.
- Larghezza occhi e loro distanza.
- Distanza degli occhi rispetto al centro di simmetria del viso.
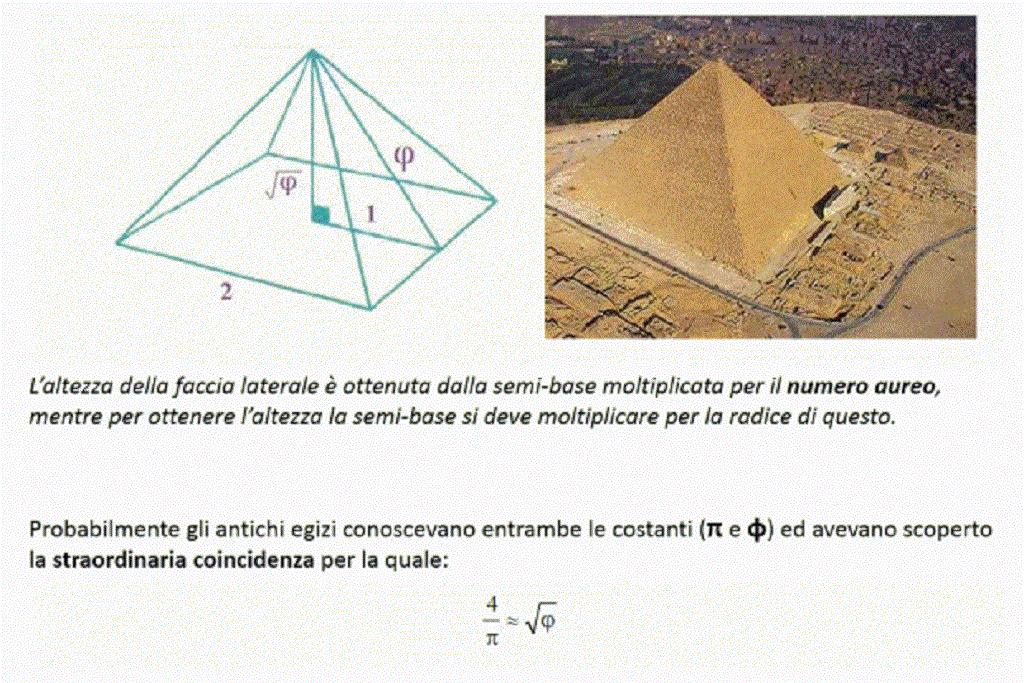
In arte e architettura il rapporto aureo è presente all’interno della Piramide di Cheope, tra il semilato della piramide e l’altezza della facciata triangolare costruibile sulla stessa, che porterebbe ad una inclinazione teorica della facciata pari a 51° 49′ circa. La piramide reale ha una altezza di 147 metri e lati di 230 metri con una inclinazione delle pareti di 51° 50′ 35”, simile in maniera pressocché estrema alla inclinazione teorica.

In epoca greca sono numerose le opere scultoree e architettoniche che rappresentano al loro interno questo rapporto aureo, considerato alla base di concetti di armonia e bellezza. Non unico esempio ci è dato dal Partenone, tempio dedicato alla dea Atena.
Allo stesso modo anche in opere pittoriche rinascimentali analoga proporzione aurea contraddistingue numerose opere. Un esempio ci è dato da una delle maggiori e più note opere di Leonardo Da Vinci, la Gioconda.

All’interno del quadro, il rapporto aureo si evidenzia nella disposizione dell’immagine, nella dimensione del viso, nell’area che va dal collo a sopra le mani, nell’area che va dalla scollatura dell’abito fin sotto le mani.
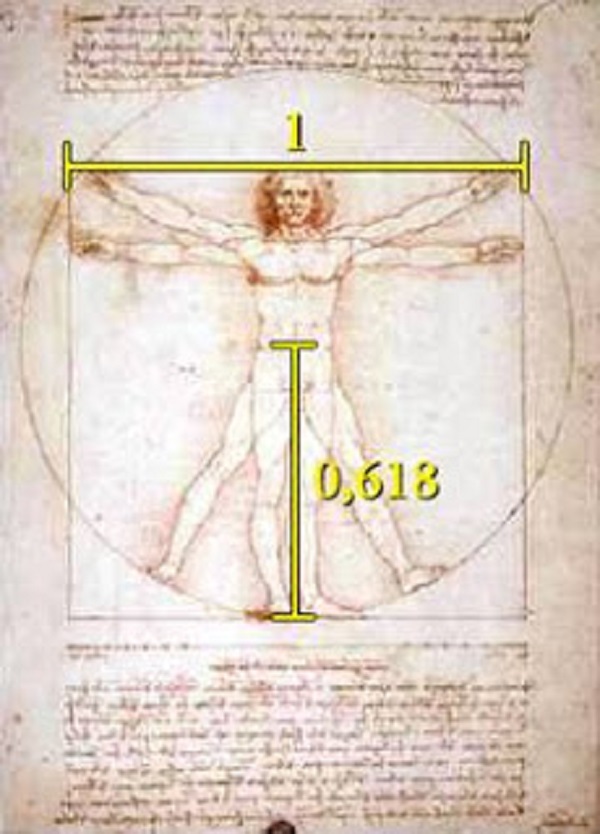
Nell’Uomo Vitruviano Leonardo studia le proporzioni della sezione aurea sulla base dei princìpi del De Architectura di Vitruvio che seguono esattamente i rapporti del numero aureo. Infatti Vitruvio scrive:
Il centro del corpo umano è inoltre per natura l’ombelico; infatti, se si sdraia un uomo sul dorso, mani e piedi allargati, e si punta un compasso sul suo ombelico, si toccherà tangenzialmente, descrivendo un cerchio, l’estremità delle dita delle sue mani e dei suoi piedi.








